Potential Energy Storage

Wherever nature offers a large height difference, the storage of potential energy can be realized at low cost. As is well known, lifting work is W pot = m · g · h = mass • acceleration due to gravity • height.

Calculation example: For every 10 meters of lifting height (and g ≈ 10 m/s²), a volume of 36m³ of water is required for W pot = 1kWh = 3.6·10 6 joules. This is not a really small volume of water, thus storage of potential energy is only worthwhile, where nature offers a decent height difference by itself, as it is the case for example with reservoirs in the mountains. (nice pictures: https://de.wikipedia.org/wiki/Stausee)

.
Standard ready to buy water pumps with efficiencies above 90 % can only be bought in the megawatt range.
see:
 
Pumps for smaller capacities have to be designed and built by ourselves. If we lift the water directly with a piston, we only have to surmount the potential energy (lifting-work) but furthermore only a minimum of friction and losses.
To develop an alternative design for pumps with a really good efficiency (not far below 100%) is not a difficult problem.
.
For re-conversion of the potential energy of water into kinetic energy and/or electric energy, it makes no sense to use water turbines like ship's propellers, because a considerable flow of water always passes them unused.
The optimum efficiency is achieved when the flowing water really converts its entire potential energy into mechanical energy. Then only the friction occurs as mechanical loss.
Similar constructions, whose efficiency is much better than the efficiency of modern water turbines, existed already some centuries ago.

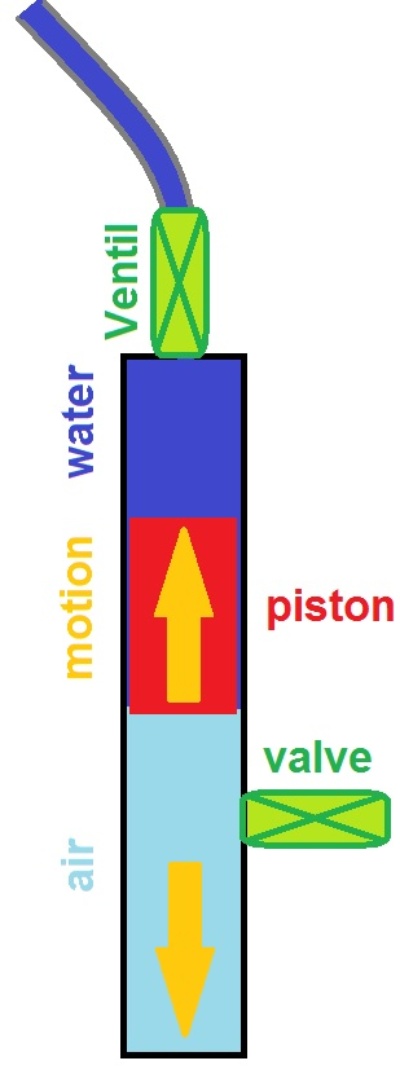
Rough estimation of the costs - just to find an order of magnitude:

On the Internet, the price for buying an alternator (electrical generator) is about 200 €, with a power of 1 kW. For larger units, the price naturally increases less than linearly with the power, so that you can get about 10 kW in the range of 500 ... 1000 €. If we assume (arbitrarily, but pessimistically) that a water pump (to lift the water) is comparable in price as the alternator, and all other components again (additionally), then we come to perhaps 2000 € ... 3000 € for a 10 kW system (in power). But this refers only to the power, as to the convertible energy per time, not to the storage capacity of the energy storage. Even if we would set the costs for the water pump and the power generator significantly higher, this would not be a problem at all in the case of large energy storages, because spoke about the costs per power, which is independent of the size of the water basin; only the latter one determines the cost of the energy storage (in kWh).

What is important for the storage capacity is the water reservoir and its size. Here comes, as said, the critical aspect: water reservoirs as energy storage always work exactly (and only) if nature provides us with a decent height difference (free of charge), so that we only need to produce the water reservoirs with an excavator. This is the crucial boundary condition, which can make the storage of energy by means of the potential energy of water extremely cost-effective under certain circumstances, possibly far below 100 € per kWh, provided that one can build it at a favourable place in the landscape.

Converting the price to cents per kilowatt-hour (see above), of course yields fantastically low values because the lifetime is not limited by a number of cycles. Because of the unlimited lifetime, this would therefore result in an energy storage price in cents per kilowatt hour that approaches down to zero in the limit value (for long time).

to top
Print